In the mind of most people, the term “exponential growth” strongly implies quick growth. However, something that grows exponentially will seem to grow quite slowly at first. In practice, there is a good chance that you won’t notice it at all until it suddenly “pops into view”. Take the adoption of something like smartphones, a typical example (I’m sure it’s not really close to exponential growth in any strict sense, but it seems a reasonable example). If the growth of smartphone usage had been linear instead of exponential, you would have noticed its importance a lot sooner, not later. Why is that? Read on for an explanation of this seemingly counterintuitive effect.
Let’s assume that you notice smarthones as a significant new thing if 10% of the people you meet has one, and that you feel that “everybody” has one when 80% does. Let’s do a numerical example for 1000 people, and assume that it takes eight years before 800 of those people (80%) has a smartphone.
Linear vs. Exponential
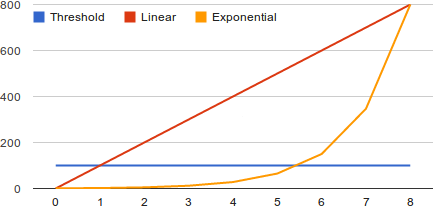 Linear vs. exponential
Linear vs. exponentialIn the linear case, 100 people switch to a smartphone each year. This means that you notice smartphones as significant after just one year, and feel that almost everyone has one after eight. There is a difference of seven years between becoming aware of the existence of smartphones and their use being ubiquitous.
In the exponential case, we assume that only one person has a smartphone in the beginning (why not zero?), and we create an exponential so that 800 people have one after eight years. Exponential growth implies that the number of users is multiplied by some number each year. How to find that number? We start from the basic formula for exponential growth,
\[x_t=x_0g^t,\]
where \(t\) represents time, \(x_0\) the initial value, \(x_t\) the value at time \(t\), and \(g\) the growth factor. We then need to compute the growth factor for reaching 800 people after eight years, starting from a single person. This means that \(x_0=1\), \(x_t=800\), and \(t=8\). By rearranging the previous equation and taking the \(t\)th root, we get
\[g=\sqrt[t]{\frac{x_t}{x_0}}=\sqrt[8]{800}\approx 2.306.\]
This means that the number of smartphone users more than doubles each year. This sounds very impressive, but it actually means that two people will have a smartphone after a year, five after two, and twelve after three, still far below the 10% threshold. The threshold (100 people) is exceeded in the sixth year, leaving only 2.5 years between awareness and ubiquitous use. If the appearance of smartphones affects you economically (say, you manufacture “dumb” phones), this means that you will have little time to adjust if you wait for them to become significant (10% of the people has made the switch) before taking action.
In general, it is much more difficult to “not miss” a phenomenon that exhibits exponential growth than one that exhibits linear growth.
Add new comment