Reconstruction of a Real Dataset, Part 4: The Actual Reconstruction

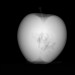
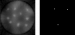
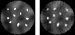
This is part four of a tutorial that describes how to create a reconstruction of a cone-beam computed tomography (CT) dataset. In this part, I’ll show how to create the actual reconstruction from the projections that were created in…