Some Mathematics Behind "Catching Them All"

Pokémon Go logo.

Mathematics is everywhere. In this article, I present some of the mathematics behind “Catching Them All”. I admit that I’ve lured you in with Pokémon Go to introduce some mathematics, but I promise that it is only very mild stuff.

Say that a rare Pokémon pops up in your Sightings (the list of nearby Pokémon in the Pokémon Go app), and that you walk in a straight line until it disappears again. What have you then learned about the position of that Pokémon?

Well, since the Pokémon is only on the list when it is closer than a given distance, and that the creature appears and disappears when you are that distance away from it, you’ve just walked on a chord of a circle with the Pokémon in the middle! This is illustrated in Figure 1; the red line is a chord of the green circle. In principle, if you know the exact diameter of the circle, then there are only two possible locations for the critter. One is in the center of the green circle and one is in the center of the dotted green circle. Given that you know the length of the chord and the diameter of the circle only approximately (the true circle might be, e.g., the dotted gray one), it is safer to say that what you’ve actually learned is that the Pokémon is on a line perpendicular to the middle of the chord, shown as the dotted red line in Figure 1.

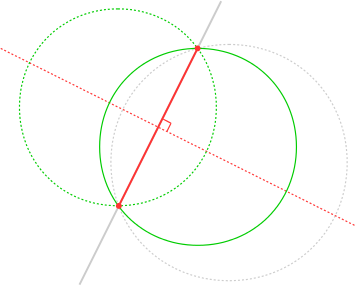Figure 1: A chord of a circle.

If, after the Pokémon has disappeared, you take a turn and walk in another straight line, then there are two possibilities. The first one is that you do not walk back into the circle, so that the Pokémon does not reappear. In that case, turn back and try again. The second possibility is that you walk on another chord of the circle. Using the two perpendicular lines in the middle, shown as the dotted red lines in Figure 2, you can then exactly determine the position of the, in this case, yellow Pikachu.

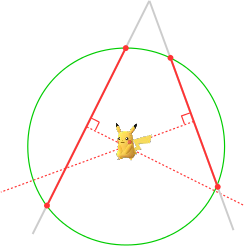Figure 2: Two chords together determine a unique point.

There are a few potential problems with this approach:

• The two chords that you’ve walked on might be for two different Pokémon of the same species, each with their own circle. However, I assume that you’ll only use techniques like this for rare species, so that shouldn’t be too much of a problem.
• When you first spot the Pokémon, it might actually have popped up just then, instead of you getting near enough to it to see it. In that case, you might need to forget the first chord and start from the second one.
• In a city, you can’t just walk in every direction that you’d like to, since there has to be an actual street there.

So, this is not a surefire technique… But, hey, we did some mathematics!