Yes, you can do symbolic math in Python! The library to take a look at is SymPy. Its official website is SymPy.org. This article is not a SymPy tutorial, as I only want to walk you through some examples to show you the kinds of things that it can do. A good place to start if you want more information is the SymPy Tutorial from the official documentation.
Now, to pick an example… Given the site that you’re reading this on, what better example to use than the sinc function, as used in the creation of windowed-sinc filters? The sinc function is defined as
\[\mathrm{sinc}(x)=\frac{\sin(\pi x)}{\pi x}.\]
This is the normalized version that is typically used in signal processing. It is normalized by multiplying \(x\) with \(\pi\). The effect of this is that the integral becomes one instead of \(\pi\), and that the zeros of the function are (all the non-zero) integer values of \(x\). The central part of the normalized sinc function is shown in Figure 1.
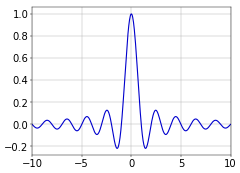 Figure 1. Normalized sinc function.
Figure 1. Normalized sinc function.In the code fragment that follows, I’ll define the sinc function in SymPy. There are lots of imported symbols in the first two lines, for the other examples that follow.
>>> from sympy import symbols, sin, pi, pprint, latex, Limit, limit, \ ... Integral, oo, integrate, diff >>> x = symbols('x') >>> sinc = sin(pi * x) / (pi * x) >>> pprint(sinc) sin(π⋅x) ──────── π⋅x
pprint() is a SymPy function that does pretty printing, as you can tell. You can also convert the output to \(\LaTeX\) using the latex() function, as follows:
>>> print(latex(sinc)) \frac{1}{\pi x} \sin{\left (\pi x \right )}
If I then put this into the current article in the usual way, it renders as
\[\frac{1}{\pi x} \sin{\left (\pi x \right )}.\]
You can then evaluate an expression by subsituting a value for one or more of the symbols. Let’s evaluate our sinc function for some values of \(x\):
>>> sinc.subs(x, 1) 0 >>> sinc.subs(x, -2) 0 >>> sinc.subs(x, 0.5) 2.0/pi >>> sinc.subs(x, 0) nan
The evaluation for \(x=0\) returns nan. This is because the sinc function has the indeterminate form of \(0/0\) at that point. Of course, since we are looking at a symbolic math toolbox, let’s compute the limit for \(x\to0\). We can first let SymPy generate the \(\LaTeX\) expression, as follows:
>>> print(latex(Limit(sinc, x, 0))) \lim_{x \to 0^+}\left(\frac{1}{\pi x} \sin{\left (\pi x \right )}\right)
This renders as
\[\lim_{x \to 0^+}\left(\frac{1}{\pi x} \sin{\left (\pi x \right )}\right),\]
but remember that you can also print it directly on your terminal screen using pprint():
>>> pprint(Limit(sinc, x, 0)) ⎛sin(π⋅x)⎞ lim ⎜────────⎟ x─→0⁺⎝ π⋅x ⎠ >>> pprint(Limit(sinc, x, 0), use_unicode=False) /sin(pi*x)\ lim |---------| x->0+\ pi*x /
The formatting with Unicode (the first pprint() statement) is not entirely correct here, but it looks really good in an actual terminal window. Not that the above code uses Limit(), with a capital L. Evaluating the limit can be done by using the limit() function (with lowercase l), or by calling the doit() member on the result of the call to Limit(). Evaluating the limit results in
>>> print(limit(sinc, x, 0)) 1
Note that this result implies that SymPy is smart enough to apply L’Hôpital’s rule, because the limit expression also results in the indeterminate form of \(0/0\). If you want to apply L’Hôpital’s rule manually, you can compute the derivative of the numerator and of the denominator and then compute the resulting limit.
>>> print(diff(sin(pi * x))) pi*cos(pi*x) >>> print(diff(pi * x)) pi >>> print(limit(diff(sin(pi * x)) / diff(pi * x), x, 0)) 1
Finally, now that we’re doing calculus anyway, let’s evaluate the integral from \(-\infty\) to \(+\infty\) of the sinc function:
>>> pprint(Integral(sinc, (x, -oo, oo))) ∞ ⌠ ⎮ sin(π⋅x) ⎮ ──────── dx ⎮ π⋅x ⌡ -∞ >>> print(integrate(sinc, (x, -oo, oo))) 1
This is the expected result. Note the cute use of oo for infinity… Anyway, do remember, for when the need arises, that you can use Python for symbolic math!
Add new comment