A constellation diagram is a diagram that shows how the information in a digital modulation scheme such as phase shift keying (PSK) is represented in a modulated carrier. This article is a bit of an experiment; instead of introducing the constellation diagram by simply presenting it, I’m going to try to have it emerge from the formulas of PSK modulation.
I’ve already mentioned the general waveform for Multiple Phase-Shift Keying (MPSK) at the end of the article mentioned above, as
\[s_m(t)=A\cos\left(2\pi f_c t+\frac{\pi(2m+1)}{M}\right),\]
for \(m=0,\ldots,M-1\). In this equation, \(A\) is the amplitude of the carrier, \(f_c\) is the frequency of the carrier, and \(M\) is the number of phase offsets. This formula represents a carrier wave of which the phase is suddenly shifted for each new symbol (if that symbol is different from the previous one, of course). This is a digital modulation scheme, because the phase is changed in fixed steps instead of continuously as for analog modulation techniques.
To get to the constellation diagram, we first switch to the analytic form of the waveform (see What is an Analytic Signal? for details), as follows.
\[\tilde{s}_m(t)=s_m(t)+i\mathcal{H}(s_m(t))\]
This results in
\[\tilde{s}_m(t)=A\cos\left(2\pi f_c t+\frac{\pi(2m+1)}{M}\right)+iA\sin\left(2\pi f_c t+\frac{\pi(2m+1)}{M}\right)\]
when applying the Hilbert transform, and finally in
\[\tilde{s}_m(t)=Ae^{\textstyle i\left(2\pi f_ct+\frac{\pi(2m+1)}{M}\right)},\]
by applying Euler’s formula. Because the waveform for MPSK is simply a cosine with a phase offset, the calculation of the analytic signal is the same as in the mentioned article on analytic signals.
The common part for the expression for each of the \(\tilde{s}_m(t)\) with \(m=0,\ldots,M-1\) is a vector of length \(A\) rotating with a constant frequency of \(f_c\), given by
\[Ae^{i2\pi f_ct}=A\cos(2\pi f_ct)+iA\sin(2\pi f_ct).\]
If you plot this on the complex plane, then you get a circle. This is not a very informative thing to do, but we are getting closer to the constellation diagram.
The key insight to get to the constellation diagram is that the analytic signal allows putting the carrier frequency \(f_c\) to zero. Of course, to do that, you have to be willing to use complex signals throughout your modem instead of real ones. This is often referred to as inphase (I) and quadrature (Q) processing, where I represents the real axis of the complex plane and Q represents the imaginary axis.
For the specific example of MPSK, setting \(f_c=0\) results in the waveform
\[\tilde{s}_m(t)=Ae^{\textstyle i\frac{\pi(2m+1)}{M}}=A\cos\left(\frac{\pi(2m+1)}{M}\right)+iA\sin\left(\frac{\pi(2m+1)}{M}\right),\]
still for \(m=0,\ldots,M-1\).
For the even more specific example of MSPK with \(M=4\), and for \(A=1\), this leads to the constellation diagram of Figure 1. Because \(A=1\), the coordinates of the top-right point, for example, are \((\sqrt{2}/2,\sqrt{2}/2)\).
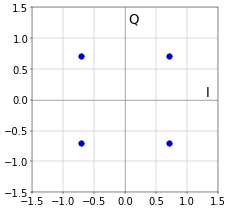 Figure 1. QPSK constellation.
Figure 1. QPSK constellation.For binary phase shift keying (BPSK), so for \(M=2\), this leads to the diagram of Figure 2.
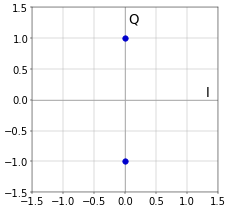 Figure 2. BPSK constellation.
Figure 2. BPSK constellation.In application such as cable or DSL modems for broadband internet, more elaborate constellations such as Quadrature Amplitude Modulation (QAM) are used. In QAM, both the phase and the amplitude of the signal are adapted in order to be able to send more bits per symbol. An example is 16-QAM (4 bits per symbol), as shown in Figure 3. Cable modems typically use 64-QAM or 256-QAM, and, for DSL, constellations as large as 32768-QAM (15 bits per symbol) are used routinely.
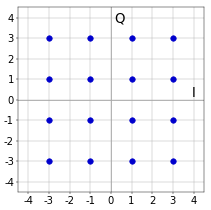 Figure 3. 16-QAM constellation.
Figure 3. 16-QAM constellation.In conclusion, a constellation diagram is a way to represent the waveforms of a digital modulation scheme in a concise way. Of course, the examples shown above are the perfect constellations. In practice, the constellation diagram is used to detect problems with the received signal, such as excessive noise or timing problems.
Add new comment