The impulse response of a system is, perhaps not entirely unexpectedly, the response of a system to an impulse. The concepts of signals and systems, in the context of discrete-time signal processing, are introduced in the article Discrete-Time Signal Processing. This article introduces the all important impulse response, and shows how knowing only the impulse response of an LTI system can be used to determine the output of that system for any given input.
Impulse
Defining an impulse in continuous-time signal processing is quite tricky. There, it is defined through the Dirac delta, which can be described as
\[\delta(x)=\begin{cases}+\infty,&x=0\\0,&x\ne 0\end{cases}\mathrm{,\quad with }\int_{-\infty}^\infty\delta(x)\,dx=1.\]
For discrete-time signal processing, things are much easier. There, an impulse is defined through the signal
\[\delta[n]=\begin{cases}1,&n=0\\0,&n\ne 0\end{cases},\]
which is called the unit sample function or, simply, impulse. The center part (since its length is infinite, albeit zero everywhere except for the origin) of this signal is shown below, with the zero time point in the middle of the graph.
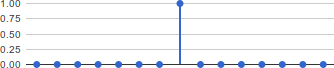 Unit sample function
Unit sample functionImpulse Response
As already noted in Discrete-Time Signal Processing, an LTI system is completely characterized by its impulse response. This means that knowing the impulse response is sufficient to completely predict what the system will output for any possible input. The impulse response is often written using the letter \(h\), as \(h[n]\). For example, the identity system has \(h[n]=\delta[n]\).
As a somewhat more complex example, consider the system for which the impulse response is shown below.
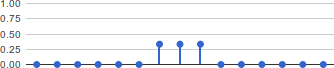 Moving average impulse response
Moving average impulse responseA system with this impulse response computes a moving average. We know the output of this system when the input is an impulse, since we know the impulse response. What is the output of the moving average system for the following signal?
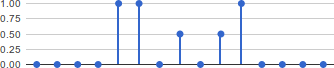 Moving average input
Moving average inputThe output is shown below. Even with these very simple signals, the relation between the input and the output is not obvious to the eye, although small examples like this could still be computed manually.
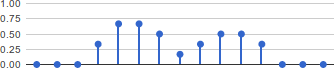 Moving average output
Moving average outputAn example with audio signals is shown in How to Record a Lion in a Concert Hall. That article shows how the impulse response of a concert hall makes it possible to compute how the roar of a lion would sound in that concert hall.
Convolution
For the specific case of an LTI system, the reaction of the system to an impulse can be computed by convolution. The convolution of two (discrete and one-dimensional) signals is defined by the infinite sum
\[(x*h)[n]\equiv\sum_{m=-\infty}^\infty\!x[m]\,h[n-m],\]
where, in this application, \(x\) is the original signal and \(h\) is the impulse response.
Computing a convolution by following this definition closely is a very expensive operation (in terms of computation). However, the ubiquitous use of convolution is enabled by the Fast Fourier Transform (FFT) algorithm.
Add new comment