There is really only one circle. Of course, you have to allow for translation and scaling for this to be true, but I think you’ll agree that a large circle is essentially the same as a small one. The geometrical term for this is similarity. Two objects are similar if they can be transformed into each other using only (uniform) scaling, translation, rotation, and reflection. This means that, for example, all squares are similar, but all ellipses are not. Figure 1 illustrates this with two circles and two ellipses. You can translate the circles so that they have the same center and then scale them to be the same size. The ellipses, however, can be translated and rotated, but the narrow ellipse cannot be scaled onto the wide one.
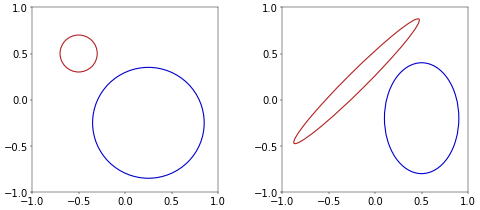 Figure 1. Circles and ellipses.
Figure 1. Circles and ellipses.The funny thing is now that all parabolas are also similar, which may be unexpected. For example, look at the two parabolas of Figure 2. They seem different in the same sense that the ellipses of Figure 1 are. But they are not (I’m sure you’ll agree that, intuitively, it is possible to translate and rotate each parabola so that it has its top (vertex) in the origin, as the two parabolas of Figure 2, so I won’t talk about that).
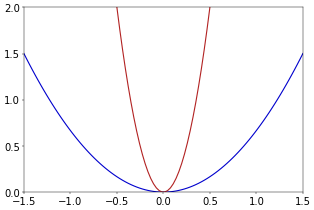 Figure 2. Parabolas.
Figure 2. Parabolas.The formulas for the two parabolas are
\[y=8x^2\]
for the red one and
\[y=\frac{2}{3}x^2\]
for the blue one. If all parabolas are similar, then that means that there exists a uniform scaling of the red parabola that puts it on top of the blue one. This scaling is
\[(x,y)\rightarrow(12x,12y).\]
This scaling puts, for example, the point \((0.5,2)\) from the red parabola on the point \((6,24)\) from the blue one.
In general, for two parabolas \(y=ax^2\) and \(y=bx^2\), the scaling is
\[(x,y)\rightarrow(\frac{b}{a}x,\frac{b}{a}y).\]
This is because applying the scaling to
\[y=ax^2\]
leads to
\[\frac{b}{a}y=a(\frac{b}{a}x)^2\]
\[\frac{b}{a}y=a\frac{b^2}{a^2}x^2\]
\[y=bx^2.\]
Hence, there’s only one parabola, in the sense that each parabola is a larger or smaller version of each other parabola (after rotation and translation).
Add new comment