Applying a Filter in Both Directions Makes it Zero Phase

I’d like to add another trick to your digital filter toolbox: when you apply any filter in both directions on your input signal, the combined filtering operation is zero phase.

As you know from Why use Symmetrical FIR Filters with an Odd Length?, FIR filters have several advantages. However, execution speed is typically not one of them. When the day comes that you need something that’s faster, you might need to switch to an IIR filter, for example, a single-pole IIR filter. However, as briefly explained in The Phase Response of a Filter, (causal) IIR filters are not linear phase. One consequence of this is that they don’t handle rising and falling edges in the input signal in the same way, as illustrated in Figure 1.

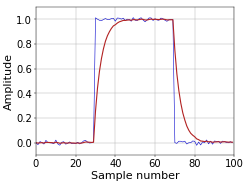Figure 1. Block pulse filtered with single-pole IIR filter.

The single-pole IIR filter is fast. Its update expression per sample is typically something like y += b * (x - y), where x is the input sample, y the output sample, and b a parameter of the filter. The value of b was 0.25 in the example of Figure 1, corresponding with a decay value of 0.75.

Apply in Both Directions

A way to work around the nonlinear phase is to apply the filter twice, both in the forward and in the reverse direction. The exact procedure to follow is the following.

1. Filter the input signal \(x[n]\). This results in an intermediate signal \(x_i[n]\).
2. Reverse the order of the samples in \(x_i[n]\).
3. Filter \(x_i[n]\) with the same filter. This results in the output signal \(y[n]\).
4. Reverse the order of the samples in \(y[n]\) to get the final output signal.

Figure 2 shows the result of following this procedure. Of course, a downside of this approach is that this filter is no longer causal. This is unavoidable, since a causal filter can never be zero phase. The non-causality is obvious in Figure 2, since the filtered signal starts to rise before the pulse arrives. This is not a problem for your further processing of the signal, but it precludes using this filter for real-time applications, at least not without introducing a delay. Which is, in turn, also no problem, since that makes the filter linear phase, which is almost always just as good as zero phase in practice.

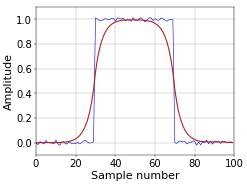Figure 2. Block pulse filtered in both directions.

Python Code

In Python, assuming an input signal x of length n and using the LowPassSinglePole class from Low-Pass Single-Pole IIR Filter, this can be implemented as follows.

# Input assumed to be in an array x of length n.
 
# Create the filter.
low_pass_single_pole = LowPassSinglePole(decay=0.75)
 
# Filter the signal.
xi = np.zeros(n)
for i in range(n):
    xi[i] = low_pass_single_pole.filter(x[i])
 
# Reverse the order of the samples.
xi = xi[::-1]
 
# Filter the signal.
y = np.zeros(n)
low_pass_single_pole.reset()
for i in range(n):
    y[i] = low_pass_single_pole.filter(xi[i])
 
# Reverse the order of the samples.
y = y[::-1]

Note that Python is definitely not the language in which this kind of implementation is efficient. The explicit for loop over the samples of the signal is a dead giveaway in this respect. If you find yourself looping over samples in Python instead of using array operations, you know that your code is probably going to be slow. So, this code is just for demonstration purposes. In C or C++, on the other hand, an implementation like this is perfectly fine.