Langton's Ant

Say that you have an ant that lives on an infinite plain with tiles that can be either black or white. The ant can move in the four main directions, and it keeps moving indefinitely, according to the following two simple rules.

1. If the tile that it is on is white, it turns 90 degrees to the right, changes the color of the tile to black, and moves forward one step.
2. If the tile that it is on is black, it turns 90 degrees to the left, changes the color of the tile to white, and moves forward one step.

This is called Langton’s ant after Christopher Langton, who is one of the founders of the field of artificial life.

Figure 1 shows an animation of the first 50 steps in the “life” of the ant (I’ve created the animation using the code from How to Create Animated GIFs with Python). The ant itself is represented by an arrow, but the main point of the animation is, of coure, the effect that the ant has on the tiles.

Figure 1. 50 steps.

The animation in Figure 1 is terribly slow, should you want to use it to convince yourself that the ant really follows the two simple rules given above. A faster animation, of the first 200 steps, is shown in Figure 2.

Figure 2. 200 steps.

Lanton’s Ant is an example of simple rules that lead to complicated behavior. The rules are strict and straightforward, but lead to a result that looks quite chaotic. Of course, there is no randomness involved, and the system is completely deterministic.

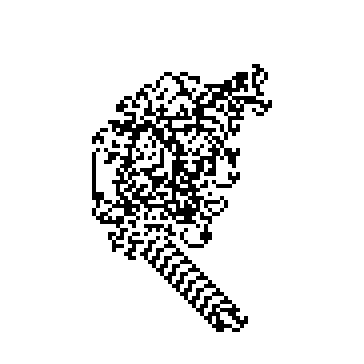Figure 3. 11000 steps.

If the animation is started from an empty plain (i.e., all tiles white) the result is that, after a considerable number of seemingly chaotic steps, the ant starts building some sort of “highway” that continues indefinitely. Figure 3 shows the result after 11000 steps.

Amazingly, it seems that every finite initial configuration of the plain leads to the ant building this exact same highway forever after a finite number of steps. Until now nobody has been able to prove this, although it has been proven that every initial configuration leads to an unbounded trajectory for the ant. As an example of this behavior I’ve created a run that started from a random tile configuration in the central 15×15 part of the plain, with the ant initially positioned in the middle (Figure 4).

Figure 4. 13000 steps from random initial configuration.