Randomness Explains Flat Tire Anecdotes Perfectly Well

Flat tires are random events. However, it seems that the human mind expects random events to be more regular than they actually are. This intuition on randomness might lead to the feeling that your own experience is somehow unexpected or strange, with anecdotes such as “my uncle seems to never have any flats, but my sister had three in the last year alone”. This is related to The Clustering Illusion, but the link between that article and you having another flat tire might not be evident.

But my Uncle Never Has any…

Flat tires are generally assumed to be Poisson distributed. To check whether the typical flat tire anecdotes can be explained by a Poisson distribution, let’s do an experiment. We’ll assume an average of one flat every five years, and plot a period of 30 years (Figure 1). There is not really a “typical” case that I can show first, since the variation between individual 30-year periods is really high. For Figure 1, I’ve just picked one of the first cases with six flat tires in the 30 year period, out of 100 runs of the experiment. It is very uncommon for the events to be evenly spread, so the “clustering” into three groups that seems apparent in this example is completely coincidental.

Figure 1. One simulated period of 30 years.

Figure 2 shows the first five of the series of 100 runs of the experiment. So these are not examples that I hand picked in some way. The number of flat tires in these five 30-year periods is 9, 3, 10, 3, and 9. This immediately shows that there is a lot of variation between the experience of different people. Without some of them needing to have a neighbor that doesn’t like them too much.

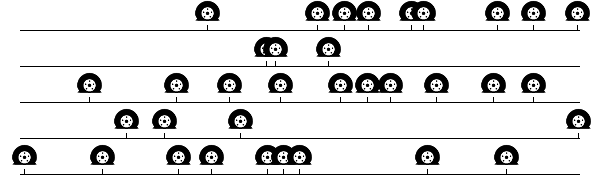Figure 2. First five simulated periods of 30 years.

To further show the large variation, I’ve assembled some “outliers” in Figure 3, all taken from 100 runs of the experiment. The first person had 15 in the 30-year period, with the first one almost immediately at the beginning of his or her “driving career”. Contrast this with the second person, who had only two, and the the third one, who had not a single flat in 30 years. The last one is really peculiar. There are a total of 10 flats, which is not really unusual. However, this person experienced two clusters of flats that were so close together that the little markers below the flat tire image only appear thicker instead of showing up as separate markers. The “second” event, e.g., is actually a cluster of three. One pixel on the scale of this bar is just over half a month, so this cluster represents three flats in the timespan of about a single month. Additionally, the “sixth” event event is also a cluster of two. Note that these outliers, as the “regular” cases above, are all without assuming any difference in, e.g., driving style.

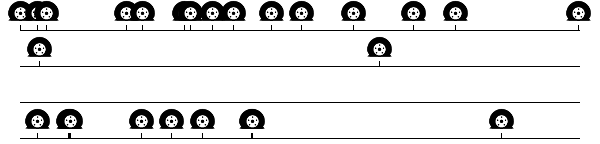Figure 3. Outlier periods.

Given all that, do you still feel that your own case is exceptional?