This article is a bit of an experiment. In it, I’ll try to explain an item from current research to the general public. I’m aware that regular readers of this blog are probably not typical elements of the set general public, but I do assume that a large majority of you is not part of the tomography research community.
In this article, I describe PDART (Partially Discrete Iterative Reconstruction Technique), which is an algorithm that I have developed during my PhD. PDART was published in 2011 (DOI: 10.1016/j.ultramic.2011.12.003).
This is the first part of a two-part article, since there was simply too much information. Also read part two.
Definition
What the PDART algorithm does is, in a nutshell, a SIRT reconstruction with intermediate segmentation steps in which prior knowledge is added to the reconstruction process.
The PDART algorithm assumes that the most dense material in the scanned object is homogeneous, and that the density of that material is known. This might seem a rather strong assumption, but there are quite a few applications for which it is true. In the mentioned journal paper, PDART was applied to catalyst and superconductor materials. Another application is segmenting bone in small animal imaging, in cases where the bone can be considered to be homogeneous.
The algorithm essentially removes the dense material from the reconstruction problem. This improves the reconstruction quality, since the densest material often causes most of the problems (such as streaks in the reconstructed image). The next section illustrates how this works.
Illustration
Figure 1 (left) shows a typical example of an object for which PDART is useful. The example is very small, only 53×53 pixels, but magnified by a factor of three for clarity. PDART also works for large reconstructions (and also in 3D), but this small and artificial example is meant to clearly shows its effect on individual pixels.
 Figure 1. Phantom image (left) and SIRT reconstruction (right).
Figure 1. Phantom image (left) and SIRT reconstruction (right).On the right is a SIRT reconstruction. The reason that the SIRT reconstruction is rather bad, is that it is based on only 25 projections. Is it possible to create a reasonable reconstruction with only these 25 projections? Let’s attempt to do just that by using PDART.
The images that follow show intermediate results. Figure 2 (left) shows the PDART reconstruction after eight iterations, which is still identical to a SIRT reconstruction after eight iterations. However, this is the iteration in which the first dense pixels are discovered, as is shown in the mask (right). The dense pixels are discovered by comparing each pixel in the image with a fixed threshold.
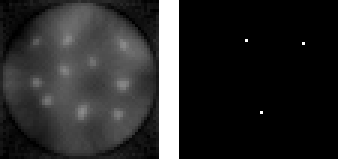 Figure 2. SIRT (left) and mask (right) at iteration 8.
Figure 2. SIRT (left) and mask (right) at iteration 8.During the following iterations, the other dense pixels are discovered one after the other. At iteration 150 (for this particular example), as shown in Figure 3, both the background and the particles are reconstructed much better than in the SIRT reconstruction of the first illustration.
 Figure 3. PDART at iterations 8 (left) and 150 (right).
Figure 3. PDART at iterations 8 (left) and 150 (right).In part two of the article, I show the mathematical details of the algorithm.
Add new comment