The PDART Algorithm, Part 2

This is the second of a two-part article on the PDART algorithm. As illustrated in part 1, PDART works by gradually removing the dense material from the reconstruction problem, thereby improving the quality of the whole reconstruction, including the dense parts. Figure 1 shows the difference with a regular SIRT reconstruction again, for the example of part 1.

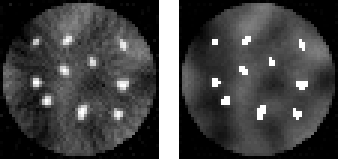Figure 1. SIRT (left) and PDART (right) reconstructions.

The PDART algorithm needs two extra input parameters to do its magic, a threshold and a gray level. After each SIRT iteration, each pixel of the intermediate reconstruction is compared with the threshold, and all pixels that exceed the threshold are fixed to the specified gray level in subsequent iterations. This fixing is done by removing the pixels from the reconstruction problem. Figure 2 is repeated from part 1, and shows how the first three dense pixels are found for this particular example.

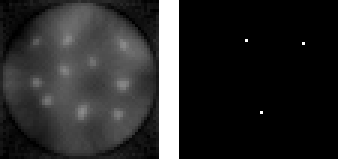Figure 2. SIRT (left) and mask (right) at iteration 8.

Note that removing does not equal forgetting, of course. The pixels are removed from subsequent iterations, but you add them back at the end, or even after each iteration if you want to view the progress in detail.

Removing Pixels

How do you remove pixels from a reconstruction problem?

Mathematically, you can write the original system of equations, \({\bf Ax}={\bf b}\) (see “Tomography, Part 4: Algebra!”), as

\[\begin{pmatrix}
\mid\! & & \!\mid\\
\mathbf{a}_1\! & \cdots & \!\mathbf{a}_n\\
\mid\! & & \!\mid
\end{pmatrix}
\,
\begin{pmatrix}
x_1\\
\vdots\\
x_n
\end{pmatrix}\!
= {\bf b}.\]

This is the same thing, but with the columns of the matrix shown individually, and with the elements of \({\bf x}\) spelled out. Removing a pixel \(x_j\) from the system of equations amounts to removing the column \({\bf a}_j\) from \({\bf A}\), together with that pixel. Of course, you then have to correct the data vector \({\bf b}\) by subtracting the contribution of the removed pixel from it. If we assume that the value of the pixel is \(\rho\) (this is simply the gray level that was chosen, of course), the new system of equations becomes

\[\begin{pmatrix}
\mid\!\!\! & & \mid\!\! & \mid\!\!\! & & \mid\\
\mathbf{a}_1\!\!\! & \cdots\!\!\! & \mathbf{a}_{j-1}\!\! & \mathbf{a}_{j+1}\!\!\! & \cdots\!\!\! & \mathbf{a}_n\\
\mid\!\!\! & & \mid\!\! & \mid\!\!\! & & \mid
\end{pmatrix}
\,
\begin{pmatrix}
x_1\\
\vdots\\
x_{j-1}\\
x_{j+1}\\
\vdots\\
x_n
\end{pmatrix}\!
= \mathbf{b} - \rho\,\mathbf{a}_j.\]

You can then repeat this for all pixels that cross the threshold, or do all of them at the same time. The final result is then a new system with the same number of equations, but with less unknowns, making the system less underdetermined. This new system of equations is then used in the following iteration. The whole process stops if no new dense pixels are found for a certain pre-determined number of iterations, or using some other stopping criterion.

The Final Result

To show the final result, as in the first image above, you have to add the dense pixels again. But that’s easy, since you know that they all have the value \(\rho\). If we add back the pixel \(x_j\) that we’ve removed in the previous expression, for example, we get

\[\begin{pmatrix}
x_1\\
\vdots\\
x_{j-1}\\
\rho\\
x_{j+1}\\
\vdots\\
x_n
\end{pmatrix}.\]

And this results in the final PDART reconstruction, when repeated for all the removed pixels.