This article contains more detailed information on setting the transition bandwidth (or roll-off) from How to Create a Simple Low-Pass Filter. That article suggest to use, as the filter length \(N\), an odd number close to \(4/b\), where \(b\) is the required transition bandwidth. This is a good basic rule. However, in my Filter Design tool, I actually don’t use 4 in the numerator of the expression, but a different value for each window type.
The information in this article is specific for windowed-sinc filters, as described in How to Create a Simple Low-Pass Filter and its sibling articles.
A Single Value for All Window Types
Rewriting the formula from the mentioned article with \(N\) on the left and with \(r\) instead of 4, since we are going to change it later, we get
\[N\approx\frac{r}{b}.\]
When a Blackman window is used, the value of \(r=4\) is a good choice. Figure 1 shows an example with a transition bandwidth of \(b=0.1\), given as normalized frequency. The red vertical lines in Figure 1 show the edges of the requested transition region of 0.1, for a low-pass filter with a cutoff point of 0.25. A filter with the requested roll-off has the edges of its transition zone close to the lines, but not outside of them. If the edges of the transition zone are farther inside, then the filter is better than requested. This is normally not a problem, but it does imply that the filter is also longer than required, which increases the computing power necessary to apply it.
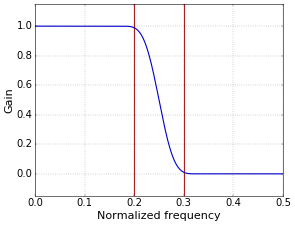 Figure 1. Low-pass filter with Blackman window, r=4.0 (filter has 41 taps).
Figure 1. Low-pass filter with Blackman window, r=4.0 (filter has 41 taps).For the Hamming and rectangular windows, the value of 4 is higher than necessary (Figure 2). Although, for the Hamming window, it is till a reasonable choice. For that reason I give a value of 4 in How to Create a Simple Low-Pass Filter, so that I don’t have to clutter that article with all the extra explanations from the current article.
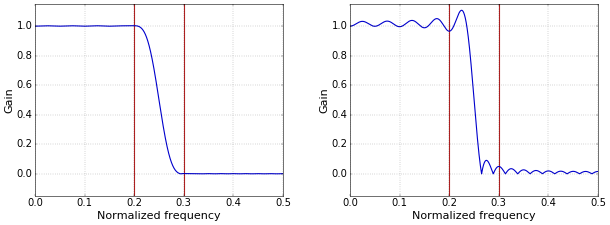 Figure 2. Left: Low-pass filter with Hamming window. Right: Low-pass filter with rectangular window. Both with r=4.0 (filters have 41 taps).
Figure 2. Left: Low-pass filter with Hamming window. Right: Low-pass filter with rectangular window. Both with r=4.0 (filters have 41 taps).A Specific Value for Each Window Type
For the Filter Design tool, I’ve used values for \(r\) that depend on on the window type. The Tool uses 4.6 for Blackman, 3.1 for Hamming, and 0.91 for rectangular. I found these values in the literature, but it is important to note that they result only approximately in the requested transition bandwidth. Moreover, other values are also found in the literature, such as 5.5 for Blackman, 3.3 for Hamming, and 0.9 for rectangular. For Blackman, a value of 4.6 results in the filter of Figure 3. Hamming and rectangular windows are illustrated in Figure 4.
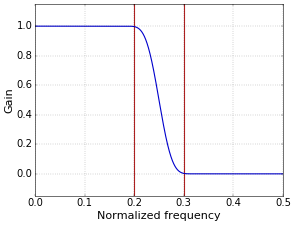 Figure 3. Low-pass filter with Blackman window, r=4.6 (filter has 47 taps).
Figure 3. Low-pass filter with Blackman window, r=4.6 (filter has 47 taps).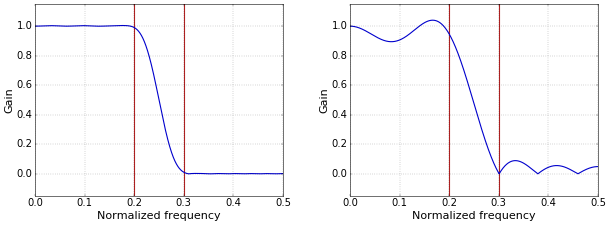 Figure 2. Left: Low-pass filter with Hamming window, r=3.1 (filter has 31 taps). Right: Low-pass filter with rectangular window, r=0.91 (filter has 11 taps).
Figure 2. Left: Low-pass filter with Hamming window, r=3.1 (filter has 31 taps). Right: Low-pass filter with rectangular window, r=0.91 (filter has 11 taps).Since even these “optimized” values are not perfect for each window type, a natural question is whether more can be done. It is clearly possible to optimize the filter length exactly, given the transition bandwidth and the criterion used to measure it. E.g., you could start from the values given above, and then vary the number of taps in steps of 2 (to keep the number odd) and check some criterion for the width of the transition region. Although, if you are willing to do all that, it might be better to switch to a more naturally configurable window type such as the Kaiser window.
Very helpful.
Add new comment