What's in a Distance

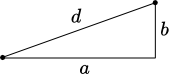
Right-angled triangle.

The distance between two points is a concept that is, in every day use, clear and unambiguous. Mathematically, the normal (every day) distance between two points is called the Euclidean distance. It is defined as

\[d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2},\]

for two points \((x_1,\,y_1)\) and \((x_2,\,y_2)\). This formula is directly based on the Pythagorean theorem,

\[d^2=a^2+b^2,\]

which states that, in a right-angled triangle, the square of the length of the hypothenuse equals the sum of the squares of the two other sides.

Let’s Generalize This!

Mathematicians that encounter the Euclidean distance as defined above immediately try to generalize it. The expression is first rewritten as

\[d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\left(|x_2-x_1|^2+|y_2-y_1|^2\right)^{1/2}.\]

In the rightmost expression, the brackets are replaced by an absolute value. This makes no difference, but is is important for the next step, which is the generalization of the exponent. Instead of using a power of two and a square root, the Minkowski distance is defined as

\[d=\left(|x_2-x_1|^p+|y_2-y_1|^p\right)^{1/p}.\]

For \(p=2\), this produces the the Euclidean distance again. This is important, since we are trying to define a generalization. But we can now choose other values for \(p\), as long as they are not smaller than one.

For \(p=1\), we get the Manhattan distance. It has this somewhat colorful name because it is the distance that a taxicab travels to get from one point to another in a cities with a grid layout, like Manhattan in New York City.

A third interesting choice is \(p=\infty\). Using infinity for \(p\) seems to be problematic at first sight, since the formula seems undefined in that case. However, we can easily solve that problem by taking the limit:

\[d=\lim_{p\to\infty}\left(|x_2-x_1|^p+|y_2-y_1|^p\right)^{1/p}.\]

The remarkable result of using \(p=\infty\) is that this leads to

\[d=\max(|x_2-x_1|,\,|y_2-y_1|).\]

So only the difference in one of the two directions is actually used! However, this expression still defines a distance, called the Chebyshev distance.

Circles?

An interesting exercise is to try to figure out how a circle looks using these alternative definitions of distances. Keep in mind that it is not the definition of the circle that changes! A circle is still the set of points that are a certain constant distance away from the center. The following figure shows unit circles using the Manhattan, Euclidean, and Chebyshev distances. A unit circle is a circle with radius one.

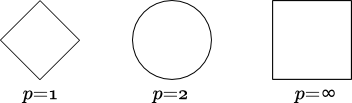Unit circles

Can you understand why these drawings are correct (i.e., go from huh? to aha!)? Can you figure out what the circumference of each of these circles is? Hint: it's \(2\pi\) for the middle one. ☺