Using modulation in radio communications is unavoidable. If, e.g., audio would be transmitted directly as a radio signal, then a single transmission would occupy the complete band, since all audio signals occupy about the same frequency range. Hence, nobody else would be able to transmit at the same time. Modulation moves the signal to (much) higher frequencies, and makes it possible to assign a different frequency to each transmitter. There is also the additional benefit that the size of an antenna is proportional to the wavelength of the signal, so that modulation enables the use of much smaller antennas.
Carrier and Message
The simplest modulation technique is Amplitude Modulation (AM), where the amplitude of a carrier is varied according to the message (e.g., a radio broadcast) that is to be transmitted. A carrier is a simple sinusoidal wave, as illustrated in Figure 1.
Figure 1. Carrier wave.In practice, a carrier such as this one would have a frequency of around 1 MHz for broadcast radio. How to transmit the following message signal by modulating the amplitude of the carrier wave?
Figure 2. Message.Amplitude Modulation
Mathematically, the modulation amounts to multiplying the carrier wave with the message. The carrier wave is defined as
\[c(t) = A\cos(2 \pi f_ct),\]
with \(A\) the amplitude of the wave and \(f_c\) the frequency. If the message is \(m(t)\), with \(|m(t)|\leq1\), then the AM-modulated carrier is given by
\[c_\mathrm{AM}(t) = (1+m(t))\,A\cos(2 \pi f_ct).\]
Adding \(1\) to the message brings it to the range \([0,2]\), so that the carrier just vanishes at the smallest message values. The result is shown in Figure 3. The original message is the envelope of the modulated carrier.
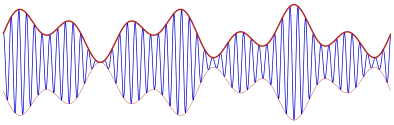Figure 3. AM-modulated carrier.In practice, the ratio between the frequency of the carrier and the frequencies that are present in the message is typically much larger than shown in this illustration. For broadcast radio, the frequency of the carrier is around 1 MHz, as mentioned before, while the frequencies in the audio signal are limited to about 10 kHz.
Although AM has been almost completely replaced by FM for radio broadcasting (there is a follow-up post on frequency modulation), it is still in use. It also has the added benefit of being the easiest of all modulation schemes to explain…
Nice notes
very good and understandable description of AM thank you
Your diagram shows maximum modulation voltage creates maximum carrier, and minimum modulation voltage creates zero carrier. It is my understanding that it is the opposite-- that is, no modulation creates maximum carrier and full modulation voltage is minimum/zero carrier. If that is the case, please fix your diagrams.
Thanks.
I don't know where you get that from, but you might simply be used to different terminology… In this article,
m(t)is the modulation voltage. When the voltage of the message is high, the amplitude of the carrier is too. In practice, for example, the simplest way to do AM demodulation (i.e., to retrieve the message from the modulated carrier) is a so-called envelope detector. This implies that the message must be modulated onto the carrier as I show in the figures.This is a great explanation of AM. I am trying to relate AM to the posts you have done on low pass and more specifically band pass filters. You said a band pass filter can be created as a low pass and high pass filter with appropriate cutoff frequencies by convolving the two filters. A band pass filter can also be constructed from two low pass filters with appropriate cutoffs. How does AM impact the component parts of a band pass filter in either of these methods? My understanding is AM will not impact the underlying frequencies but it could change the filter output slightly in the time domain. Would two windowed sinc low pass filters or two centered MA filters incorporate a good portion of AM so I don't have to worry about when constructing a BP filter? It seems like a lot of trouble for a small increase in accuracy of the filter output in the time domain.
Add new comment