Say that you have implemented a low-pass FIR filter with the correct cut-off frequency and transition band, but that you are not quite happy with the suppression of frequencies in the stop band. Figure 1 shows the impulse and frequency responses of the example filter from How to Create a Simple Low-Pass Filter.
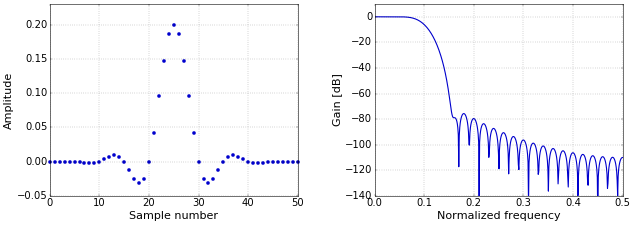 Figure 1. Impulse (left) and frequency (right) responses of a low-pass FIR filter.
Figure 1. Impulse (left) and frequency (right) responses of a low-pass FIR filter.This is a relatively short filter with 51 coefficients. The length of the filter determines the width of the transition band, and the window that is applied to the filter coefficients determines the suppression in the stop band. This means that you cannot improve the suppression by simply increasing the length of a filter designed in this way, since that would only make the transition band narrower.
Apply the Filter Twice
A straightforward trick to put in your toolbox is that you can double the suppression by applying the filter twice. This is intuitively obvious, since the filter decreases the power level in its stop-band frequencies by a certain level, and feeding it a signal with a low signal power in that region doesn’t change that. Figure 2 shows the frequency response that you get when you apply the filter of Figure 1 twice.
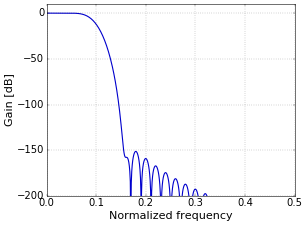 Figure 2. Frequency response of applying the filter of Figure 1 twice.
Figure 2. Frequency response of applying the filter of Figure 1 twice.The already generous 74 dB of suppression that results from using a Blackman window in the original filter is doubled.
Convolve the Filter with Itself
Instead of applying the filter twice and be done with it, there is an additional trick that you can apply. You can convolve the filter with itself to compute a new filter that has exactly the same effect, due to the associativity of convolution. If you call the input signal \(s\) and the filter \(h\), then applying the filter twice can be written as \((s*h)*h\), which has the same effect as \(s*(h*h)\), where \(h*h\) is the filter convolved with itself. Figure 3 shows the impulse response of the filter of Figure 1 convolved with itself.
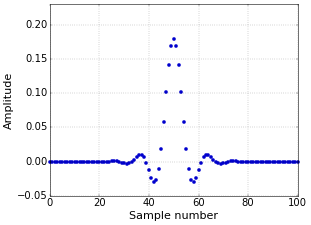 Figure 3. Impulse response of the filter of Figure 1 convolved with itself.
Figure 3. Impulse response of the filter of Figure 1 convolved with itself.Of course, the price to pay is that the filter is now longer. Convolving two filters of length 51 results in a filter of length 101. This is because convolving two signals of length \(N\) and \(M\) results in a new signal of length \(N+M-1\). Using this new filter is not necessarily faster, but it might be more convenient. If you apply the filter in the frequency domain through a Fast Fourier transform, then using the new filter will be faster, since applying a long filter takes the same amount of time as a short one (at least if the input signal is longer than the filter, which is normally always the case). But that is for a future article.
Python Code
The Python code that convolves the filter with itself is brief.
import numpy as np # Code to create a filter and put the coefficients in h. # ... # Convolve the filter with itself. h2 = np.convolve(h, h)
As always, applying this new filter \(h_2\) to a signal \(s\) by convolving both sequences can then be as simple as writing the following single line.
s = np.convolve(s, h2)
It sounds like you are basically talking about smoothing the filter output here. What about applying a shorter version of the filter as a smoother? This would reduce the delay from applying the original filter twice. Then the question is how do you determine the smoothing filter length? Trial and error? You could also just reduce the sampling rate to get smoother filter output.
Applying a filter twice (or convolving the filter with itself and then applying it, which has the exact same effect) has the effect of making the filter operation stronger, not smoothing the output. So, if the filter is low-pass, then applying it twice will suppress the high frequencies much more than applying it once, but the output of the filter will not be smoothed in the sense of a moving average filter smoothing the output.
Add new comment