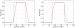
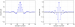
How to Create a Fractional-Delay Filter

With fractional delay, I mean a delay of a fraction of a sampling period. Introducing a delay of an integer number of samples is easy, since you can do that by simply skipping a number of samples, or buffering them if you don’t want to…