Happy Valentine’s Day! This is a bit of a trick post; after luring you in with the cute heart, I’ll explain in this article how image filtering can be implemented in frequency space…

After deciding on the name, “Impulse Response”, for my consultancy company, the next step was to create a suitable logo for it. As I’ve explained before, impulse response is a basic concept from signal and image processing. For the logo, I wanted…

There is a fundamental difference between adding Gaussian noise and applying Poisson noise. In practice, people often talk about adding Poisson noise anyway, but this is not accurate. I will be looking at this from the image processing perspective in this article, and I’ll show purely visual examples. An application of this could be…

This article is a wrap-up of what happened on TomRoelandts.com in 2013.

When taking a picture with a camera, the “true” image is convolved with the point spread function (PSF) of that camera, potentially producing a blurred image. Deconvolution is the process of removing the effect of this PSF again. In this article, I demonstrate that this is not an easy thing to do…

The most common size of ISO A series paper is A4, of which the exact size is 210 × 297 mm. How is that size determined? Amazingly, you can exactly compute all the sizes of the A series sheets from the following two simple rules…

A spectrogram is a graph that shows the evolution of the spectrum (the frequency contents) of a signal over time. Often, the frequency is on the vertical axis and time is on the horizontal axis. A spectrogram is computed by “chopping up” the signal into chunks and computing…

After introducing finite-bandwidth square waves in previous articles, I’ll now describe what happens if you follow the naive approach, and just alternate sequences of 1’s and −1’s. As you might expect after reading the previous articles, there are several problems with this. The first problem is that the naive square wave is…

After introducing the finite-bandwidth square wave in a previous article, I’ll show in this one how such a square wave looks in a digital system, so in sampled form. The figure below shows one period of a square wave of 1 kHz, sampled at 44.1 kHz, a widely used…

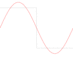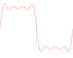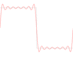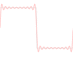
How would you produce a square wave on a digital system? At first sight, this seems completely trivial. You might think that you could just alternate a series of +1 values with a series of −1 values and be done with it. Well, it doesn’t work like that. An ideal square wave needs infinite bandwith, so creating one is…